La derniere classe nous avons introduit un élément du traitement relativement simple modelé après les unités de l'informatique de base du cerveau humain (le neurone). Nous avons appelé ces éléments les ULSs (les Unités de la Logique du Seuil).
Il y a plusieurs avantages à utiliser ces unités:
Cependant, la dernière classe nous avons vu qu'un ULS seul peut être utilisé pour modeler des fonctions simples tel que logiquement AND.
Un réseau avec seulement un ULS est très limité. Par exemple, une réseaux avec deux entrée ne peuvent pas se rapprocher une fonction XOR (ou XNOR):
| x1 | y | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nous pouvons représenter cette fonction comme graphiquement comme:
Le problème avec la fonction XOR est que ce n'est pas seperable linéairement - nous ne pouvons pas dessiner de ligne droite qui seperates les points verts des points rouges.
Comment est-ce que nous pouvons manier des fonctions plus complexes?
Nous pouvons combiner les ULSs (Unités de la Logique du Seuil) ensemble tel que la production d'un ULS crée l'entrée pour un autre:
Notez l'usage de la barrière AND - c'est la fonction que nous avons modelé dans classe 1!
En introduisant une couche intermédiaire de noeuds dans le réseau, nous pouvons former le réseau à peform tâches de la reconnaissance plus complexes (même les problèmes qui ne sont pas des seperable linéairement). C'est le domaine des réseaux multi-couche.
Fondamentalement, les noeuds additionneurs au réseau nous permettent de dessiner plus de lignes pour grouper les productions désirées ensemble:
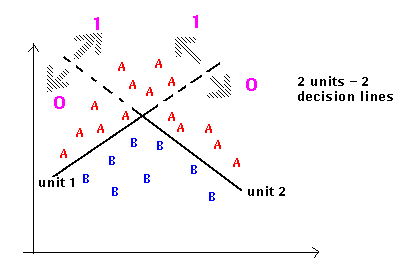
Par example, avec beaucoup d'unités cachées nous pouvons créer une surface de la décision complexe tel que:
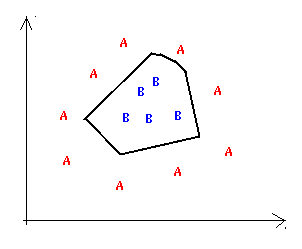
Caractéristiques Principales:
Aussi, le comportement de ces unités est appris automatiquement!
(par exemples: reconnaissez le nombre 7 - un noeud caché peut détecter une ligne verticale ou diagonale)
Par exemples, un petit réseau avec une couche intermédiaires (une couche cachée) avec 2 noeuds, et 4 sorties:
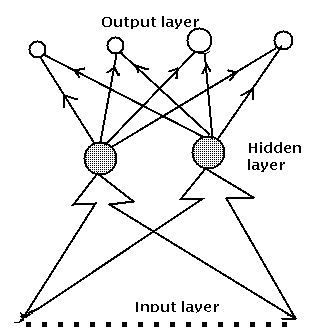
Le problème est comment former les réseaux multi-couches. Comment est-ce que nous étendons l'algorithme de base introduit pour le ULS à un réseau des ULSs avec beaucoup d'entrées, productions et couches intermédiaires de noeuds?
En premier, c'est important que nous utilisons des vecteurs - il peut y avoir beaucoup de noeuds de la production, et nous devons déterminer quels noeuds contribuent (et dans quelle direction) à l'erreur. Minimiser l'erreur de la production exige que nous considérons les poids pour tous les noeuds dans chaque couche - nous ne pouvons pas considérer juste un noeud à la fois.
Nous ferons usage étendu du "produit intérieur" pour comparer les vecteurs.
Le rappel:
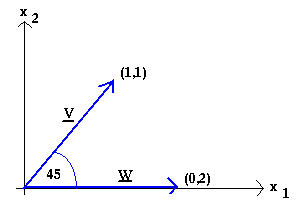
v.w = v1w1 + v2w2 = 2
Aussi:
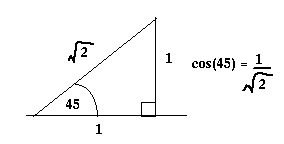
v.w = |v||w|cos(theta) = sqr(2)*2*cos(45)
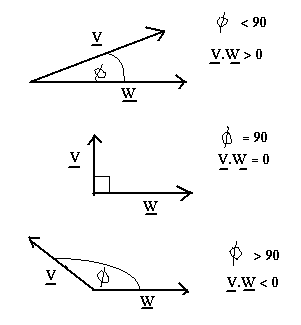
Essentiellement, le produit intérieur nous dit comme bien deux vecteurs sont alignés. Ce sera très utile quand a comparé la production courante du réseau avec la production désirée.
L'idée est à calculer une erreur chaque temps le réseau est présenté avec un vecteur de la formation et exécuter une origine de l'inclinaison (gradient descent en anglais) sur l'erreur ont considéré comme fonction des poids. Il y aura une inclinaison ou incliner pour chaque poids. Donc, nous trouvons les poids qui donnent l'erreur minime.
Par exemples, un graphique du vecteur du poids contre l'erreur:
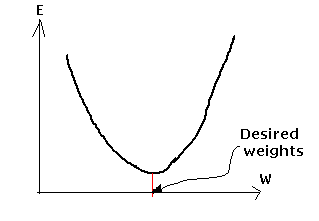
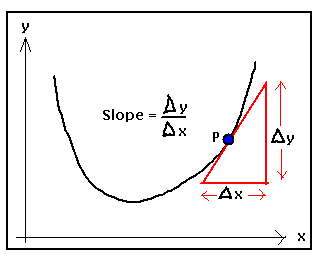
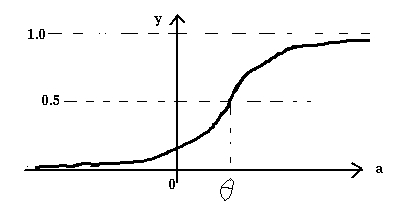
Maintenant pour exécuter l'origine de l'inclinaison, l'erreur doit être une fonction continue et differentiable des poids et il doit y avoir une inclinaison bien définie à chaque point. Mais, pendant la dernière classe nous avons défini la fonction de la sortie (y) comme:
y = 1 si a est plus que le seuil (theta) et
y = 0 si a est moins du seuil (theta) ou
Pour les réseaux multi-couche, nous allons utiliser une nouvelle fonction de l'activation qui est continue et differentiable. C'est la fonction du sigmoid:
Le 'perceptron' qui apprend la règle a été développé par Frank Rosenblatt dans les 1950s. Modèles de la formation tardifs originalement est présenté aux entrées du réseau; la production est calculé. Et puis, les poids des rapports (wj) sont modifié par un montant de qui est proportionnel au produit de:
L'algorithme est comme suit:
(commencer à la première couche et calculer la production dans chaque couche consécutive)
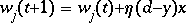
où:
(Une valeur raisonnable est 0.35)
Les pas de la répétition 2 et 3 jusqu'à:
Remarquez:
Quand nous ajustons les poids, nous commençons en calculant l'erreur à la production et ajustons les poids entre la dernière couche intermédiaire et la couche de la sortie (utilisons la fonction w(t+1) = w(t) + n(d-y)x ). Mais common est-ce que nous pouvons calculer l'erreur pour une couche intermediare?
Pour un vecteur de la sortie désiré (d), nous pouvons utiliser les poids entre la sortie et la couche intermediare à temps t pour calculer comme la production des noeuds intermédiaires doit changer dans ordre pour le réseau à production le vecteur désiré.
Pendant former, c'est souvent utile à mesurer la performance du réseau comme il essaie de trouver l'ensemble du poids optimal. Une mesure de l'erreur commune ou fonction du coût utilisées sont erreur somme - rendue carré (sum-squared en anglais). Il est calculé sur tout des vecteurs de l'entrée/production dans la formation mise et est donné par l'équation dessous:
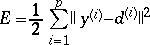
où p est le nombre de vecteur de l'input/output assortit dans l'ensemble de la formation.
Le réseau apprend en étant dit quand il a été fait des erreurs (a surveillé l'érudition).
Si une unité de la production donne la réponse mal, l'erreur est propagée arrière en bas le réseau, en produisant le poids change dans tous les liens qui ont produit la réponse mal.
Voir page 504 de (Rich et Knight, 1991) pour un algorithme plus détaillé spécifique à un reséau avec 3 couches.
Des problèmes potentiels:
1) Existence de minima local dans la surface de l'erreur:
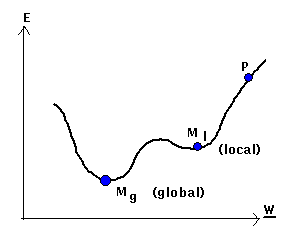
Un réseau peut glisser en bas la surface de l'erreur dans un ensemble de poids qui ne résolvent pas le problème sur quoi il est formé. Si cet ensemble de poids est un minima local, le réseau n'arrivera jamais à l'ensemble optimal de poids qui résolvent le problème.
Des solutions:
Considérez une balle dans une boîte noire. Il y a une surface à l'intérieur de la boîte et nous voulons à rouler la balle dans la vallée la plus profonde - mais nous ne pouvons pas voir à l'intérieur de la boîte. La solution est basée sur secouer la boîte.
Si nous secouons trop violemment, la balle sautera de vallée à vallée au hasard. Si nous secouons à doucement, la balle peut rester mis dans une vallée locale. La recuite simulée implique secouer la boîte très en premier fondamentalement, en ralentissant alors. À un point, la probabilité de que la balle sautera de A à B sera plus grand que la probabilité à que la balle sautera de B à A, et comme le secouer devient plus doux, la balle sera incapable de s'échapper de vallée B. Nous mettons notre foi dans les probabilités mais dans entraînement cette technique est très efficace.
2) Vitesse lente d'apprendre (mais c'est biologiquement plausible!)
3) N'augmentez pas très bien - le nombre des exemples pour former est superlinear avec la dimension du réseau
Generalization:
Si tout les entrées et productions possibles sont montrées à un réseau rétro-propagation, le réseau veut (probablement, finalement) trouvez un ensemble de poids qui dressent une carte de les entrées sur les productions. Cependant, nous ne savons pas tous des entrées possibles pour beaucoup de problèmes IA, (eg. visage et reconnaissance du caractère).
Une force majeure des réseaux neuraux est leur capacité de généraliser.
(utilisez l'exemple de reconnaître une lettre A).
Malheureusement, nous pouvons tomber aussi sur problèmes avec généralisation: (Voir page 508 de Rich et Knight, 1991)
Comme faites nous prévenons notre réseau de devenir un dictionnaire de l'entrée - production (table-lookup en anglais):
Les classes et le travaux practique étaient au sujet des réseaux multi-couche que nous formons utiliser l'algorithme rétro-propagation. Mais, il y a des autres types de réseaux neuraux, quelques-uns avec les candidatures très différentes. Je crois que Prof. Manso va parler de ces réseaux dans une classes après le congé.
Travaux Practique - Lettres d'espace
préparé février 2001 par David Croft